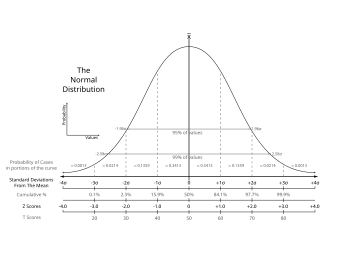
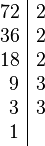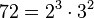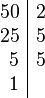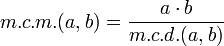La estadística es una ciencia referente a la recolección, análisis e interpretación de datos, ya sea para ayudar en la resolución de la toma de decisiones o para explicar condiciones regulares o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma aleatoria o condicional. Sin embargo estadística es mucho más que eso, dado que en otras palabras es el vehículo que permite llevar a cabo el proceso relacionado con la investigación científica.
También se denominan estadísticas (en plural) a los datos estadísticos.
Es transversal a una amplia variedad de disciplinas, desde la física hasta las ciencias sociales, desde las ciencias de la salud hasta el control de calidad. Se usa para la toma de decisiones en áreas de negocios o instituciones gubernamentales
martes, 26 de octubre de 2010
viernes, 15 de octubre de 2010
Minimo comun multiplo y Maximo comun divisor
Mínimo común múltiplo
El mínimo común múltiplo (m.c.m.) de dos o más números naturales es el menor número natural que es múltiplo de todos ellos. Sólo se aplica con números naturales, es decir, no se usan decimales ni números negativos
Cálculo del m.c.m
Partiendo de dos o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el mcm de 72 y 50 será:

Conociendo el máximo común divisor de dos números, se puede calcular el mínimo común múltiplo de ellos, que será el producto de ambos dividido entre su máximo común diviso
.
Propiedades básicas.
1
ejemplos
Allar el m c m de 30y 45
Allar el m c m de 30y 45
30 2
15 3
5 5
1
30 = 2 x 3 x 5
45 3
15 3
5 5 45 = 32 x 5
m.c.m. (30, 45) = 2 x 32 x 5 = 90
lunes, 4 de octubre de 2010
PORCENTAJE
Porcentaje
En matemáticas, un porcentaje es una forma de expresar un número como una fracción de 100 (por ciento, que significa “de cada 100”). Es a menudo denotado utilizando el signo porcentaje %, que se debe escribir inmediatamente después del número al que se refiere, sin dejar espacio de separación.Por ejemplo: "treinta y dos por ciento" se representa mediante 32% y significa 'treinta y dos de cada cien'.
El símbolo % es una forma estilizada de los dos ceros. Evolucionó a partir de un símbolo similar sólo que presentaba una línea horizontal en lugar de diagonal (c. 1650), que a su vez proviene de un símbolo que representaba "P cento" (c. 1425).
El porcentaje es un tanto por ciento (cien unidades), por lo que se concluye que es una cantidad que corresponde proporcionalmente a una parte de cien.
Representación del tanto por ciento como fracción.
El tanto por ciento se divide entre 100 y se simplifica la fracción. Ejemplo:Para saber como se representa el 10% en fracción se divide y luego se simplifica:
Representación de una fracción común como porcentaje.
La fracción común se multiplica por 100 y se resuelve la operación, como resultado será el porcentaje.Ejemplo: Para representar 1/10 como un porcentaje se hace la operación siguiente:
Obtener un tanto por ciento de un número
Para obtener un tanto por ciento se construye una regla de tres simple. Ejemplo:Para calcular el 25% de 150 se forma la regla de tres:
martes, 21 de septiembre de 2010
REGLA DE TRES
REGLA DE TRES SIMPLE
Regla de tres
La regla de tres es una forma de resolución de problemas de proporcionalidad entre tres o más valores conocidos y una incógnita. En ella se establece una relación de linealidad (proporcionalidad) entre los valores involucrados. La regla de tres más conocida es la regla de tres simple directa, si bien resulta muy práctico conocer la regla de tres simple inversa y la regla de tres compuesta, pues son de sencillo manejo y pueden utilizarse para la resolución de problemas cotidianos de manera efectiva.
Imaginemos que se nos plantea lo siguiente:
Formalizado, como antes:
Regla de tres simple directa
La regla de tres es una forma de resolución de problemas de proporcionalidad entre tres o más valores conocidos y una incógnita. En ella se establece una relación de linealidad (proporcionalidad) entre los valores involucrados. La regla de tres más conocida es la regla de tres simple directa, si bien resulta muy práctico conocer la regla de tres simple inversa y la regla de tres compuesta, pues son de sencillo manejo y pueden utilizarse para la resolución de problemas cotidianos de manera efectiva.Imaginemos que se nos plantea lo siguiente:
Problema a resolver: si necesito 2 litros de pintura para pintar 2 habitaciones, ¿cuántos litros necesito para pintar 7 habitaciones?
2 habitaciones son a 2 litros como 7 habitaciones son a Y litros.
A es a B como X es a Y
Regla de tres simple inversa
En la regla de tres simple directa, cuando el tercer término (X) crece, también crece el término que intentamos averiguar (Y), y viceversa. En el ejemplo anterior, cuando el número de habitaciones aumenta, es obvio que necesitaremos más pintura, y cuando el número de habitaciones es menor, necesitaremos menos pintura. Es lo que se llama una relación directamente proporcional. Sin embargo la vida cotidiana puede ofrecer situaciones en las cuales la relación sea inversamente proporcional, es decir, si aumenta X, entonces Y disminuye, y viceversa. Veamos el siguiente ejemplo:Problema a resolver: si 8 trabajadores construyen un muro en 10 horas, ¿cuánto tardarán 5 obreros en levantar el mismo muro?
8 trabajadores son a 10 horas, como 5 trabajadores son a Y horas.
Formalizado, como antes:
A es a B como X es a Y
FIGURAS GEOMETRICAS
POLIGONOS
Un polígono es una figura geométrica formada por segmentos consecutivos no alineados, llamados lados.
Existe la posibilidad de configurar polígonos en más de dos dimensiones. La generalización de un polígono en tres dimensiones se denomina poliedro, en cuatro dimensiones se llama polícoro, y en n dimensiones se denomina politopo.
ELEMENTOS DE UN POLIGONO
En un polígono podemos distinguir:
- Lado, L: es cada uno de los segmentos que conforman el polígono.
- Vértice, V: el punto de unión de dos lados consecutivos.
- Diagonal, D: segmento que une dos vértices no contiguos.
- Perímetro, P: es la suma de todos sus lados.
- Ángulo interior, AI: es el formado por los lados consecutivos; este se determina restando a 180º el ángulo central.
En un polígono regular podemos distinguir, además:
- Centro, C: el punto equidistante de todos los vértices y lados.
- Apotema, a: segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
- Total de diagonales, N(N-3)/2: N es el numero de lados del polígono.
Clasificación
Clasificación de polígonos según el número de lados | ||
|---|---|---|
Nombre | nº lados | |
| trígono, triángulo | 3 | |
| tetrágono, cuadrángulo, cuadrilátero | 4 | |
| pentágono | 5 | |
| hexágono | 6 | |
| heptágono | 7 | |
| octágono | 8 | |
| eneágono | 9 | |
| decágono | 10 | |
| endecágono | 11 | |
| dodecágono | 12 | |
| tridecágono | 13 | |
| tetradecágono | 14 | |
| pentadecágono | 15 | |
| hexadecágono | 16 | |
| heptadecágono | 17 | |
| octodecágono | 18 | |
| eneadecágono | 19 | |
| isodecágono, icoságono | 20 | |
| triacontágono | 30 | |
| tetracontágono | 40 | |
| pentacontágono | 50 | |
| hexacontágono | 60 | |
| heptacontágono | 70 | |
| octacontágono | 80 | |
| eneacontágono | 90 | |
| hectágono | 100 | |
| chiliágono | 1.000 | |
| miriágono | 10.000 | |
| decemiriágono | 100.000 | |
| hecatomiriágono, megágono | 1.000.000 | |
Los polígonos se clasifican por el número de sus lados según la tabla adjunta.
Se clasifican por la forma de su contorno:
|
- simple, si dos de sus aristas no consecutivas no se intersecan (cortan),
- complejo, si dos de sus aristas no consecutivas se intersecan;
- convexo, si al atravesarlo una recta lo corta en un máximo de dos puntos,
- cóncavo, si al atravesarlo una recta puede cortarlo en más de dos puntos;
- regular, si tiene sus ángulos y sus lados iguales,
- irregular, si tiene sus ángulos y lados desiguales;
- equilátero, el que tiene todos sus lados iguales,
- equiángulo, el que tiene todos sus ángulos iguales.
Poligonal
Se denomina línea poligonal al conjunto ordenado de segmentos tales que, el extremo de uno de ellos coincide con el origen del segmento que le sigue. Un polígono está conformado por una línea poligonal cerrada.POTENCIACION
POTENCIACION
La potenciación es una expresión matemática que incluye dos términos denominados: base a y exponente n. Se escribe an, y se lee: «a elevado a n».
Su definición varía según el conjunto numérico al que pertenezca el exponente:
Su definición varía según el conjunto numérico al que pertenezca el exponente:
Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.
Por ejemplo:  .
.
 .
.
cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.
cuando el exponente es una fracción irreducible n/m, equivale a una raíz:
![a^{\frac{n}{m}} = \sqrt[m]{a^n}](http://upload.wikimedia.org/math/3/9/8/3983643a5db08e21da69fffabbc0875c.png)
Cualquier número elevado a 0 equivale a 1, excepto el caso particular de 00 que, en principio, es una indefinición.La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales.
domingo, 19 de septiembre de 2010
CAPACIDAD Y VOLUMEN
Cuando queremos medir algo tenemos que elegir la unidad de medida adecuada y los instrumentos que nos posibiliten una mayor precisión. Por ejemplo, no podríamos medir el largo del salón de clase usando como unidad el kilogramo, ni decir cuánto pesa un elefante usando el litro o el metro. Del mismo modo, si un joyero necesita saber el peso de un anillo de oro precisa una aproximación mucho más fina que la del vendedor que pesa una bolsa de papas.
No nos olvidemos que los resultados de las mediciones son siempre aproximaciones, los valores que se obtienen dependen de la habilidad de la persona que mide y de la precisión del instrumento del que se disponga.
La forma de algunos objetos les permite contener sustancias; esos objetos se llaman recipientes y de ellos se puede medir tanto su capacidad como su volumen. También se puede conocer el volumen de su contenido. Por ejemplo, una taza vacía tiene un volumen, ocupa un lugar en el espacio y, como es un recipiente, también se puede medir su capacidad y el volumen del líquido que contenga. En cambio, de otros objetos, por ejemplo una piedra, sólo se puede medir su volumen. La piedra no es un recipiente.
Tanto las unidades de capacidad como las de volumen, indican de manera diferente cuál es el tamaño de un recipiente. Es importante que sepas que todos los objetos tienen un volumen ya que todos ocupan un lugar en el espacio.
La medida de una cantidad es el número de veces que esa cantidad contiene la unidad elegida. La medida se obtiene eligiendo una unidad de medida, que es la cantidad tomada como referencia para medir.
Cada magnitud tiene sus propias unidades de medida. Luego se compara la cantidad a medir con la unidad elegida y se obtiene el valor de la cantidad, o sea el número de unidades que contiene esa cantidad.
Cada magnitud tiene sus propias unidades de medida. Luego se compara la cantidad a medir con la unidad elegida y se obtiene el valor de la cantidad, o sea el número de unidades que contiene esa cantidad.
| Producto | Valor de la cantidad | Unidad de medida | Magnitud |
| Agua mineral | 500 | centímetro cúbico | volumen |
| Bebida cola | 1,5 | litro | capacidad |
Por ejemplo: en el primer caso, la magnitud medida es el volumen, la unidad elegida es el centímetro cúbico y el valor de la cantidad medida es 500 cm3.
La capacidad indica cuánto puede contener o guardar un recipiente. Generalmente se expresa en litros (l) y mililitros (ml).
El volumen indica cuánto espacio ocupa un objeto. Generalmente se expresa en metros
cúbicos (m3) y centímetros cúbicos (cm3).
Un cubito de 1 cm de arista ocupa un volumen de 1 cm3
lunes, 13 de septiembre de 2010
OPÉRACIONES CON NÚMEROS DECIMALES
OPERACIONES CON DECIMALES
Para sumar o restar números decimales, podemos hacerlo en forma de fracción y en forma decimal.
Para sumar o restar en forma decimal se colocan los números de modo que las comas estén encolumnadas. Luego se suman o restan como si fueran números naturales, poniendo la coma en el resultado en su columna correspondiente.
Para multiplicar dos números decimales, se realiza la multiplicación de ambos como si fueran números naturales. Luego se coloca la coma en el resultado, separando tantas cifras como decimales tengan en conjunto los dos factores.
Suscribirse a:
Entradas (Atom)